In a previous post, I wrote: Children need practice with a wide variety of basic computation skills.
In a previous post, I wrote: Children need practice with a wide variety of basic computation skills.
One of the basic skills listed was: Paper-and-pencil computation.
But which methods of paper-and-pencil computation?
Let’s look at multiplication, as an example.
Multiplication
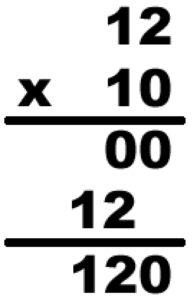
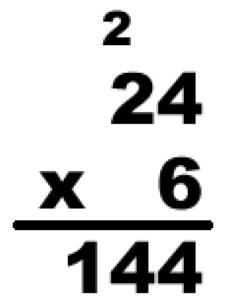 Most parents I meet learned the multiplication method shown on the right.
Most parents I meet learned the multiplication method shown on the right.
Here’s the sequence of steps:
- 6 times 4 is 24
- write the 4
- carry the 2
- 6 times 2 is 12
- add the 2 we carried to get 14
- write the 14
This method has some advantages:
 every multiplication we do involves only single digits
every multiplication we do involves only single digits
- you can multiply very large numbers by only knowing your nines multiplication table
- it always works the same way
- regardless of how big the numbers are, the process is always the same
- it’s concise and efficient
- if you have a job where you have to do a lot of multiplications every day, and you don’t have access to a calculator, this method is an asset
It also has some disadvantages:
- it un-teaches place value
- before learning to multiply, children learn that 24 is 20 + 4 (or that 24 is 2 tens and 4 ones)
- using this multiplication method, children practice calling numbers by the wrong names
- for example, when we say “6 times 2 is 12”, the 2 is really 20 and the 12 is really 120
- similarly, when we say “carry the 2”, the 2 is really 20
- the method gives the correct answer even if you don’t understand
- in other words, you don’t have to have good number sense to make it work
- which also means that practicing this method does not help develop your number sense
- for example, I once received a package where on it somebody had computed 10 x 12, as shown at right
- this is why when you ask adults to explain this method, they often can’t: they learned it as a set of rules without conceptual understanding
- it does not have a mathematical future
- because the method breaks math rules (calling numbers by their wrong names), you can’t make connections to other math children have to learn (unless that math also breaks math rules the same way)
Because of the conceptual disadvantages, some education jurisdictions are hesitant to teach such paper-and-pencil computation methods to young children.
However, this does not mean that all paper-and-pencil computation methods have these disadvantages.
Let’s look at an example for multiplication:
Multiplication v.2
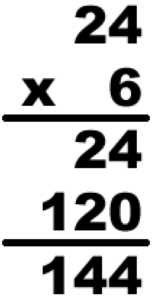 Let’s multiply 6 x 24 using a different computation method, as shown at right.
Let’s multiply 6 x 24 using a different computation method, as shown at right.
Here’s the sequence of steps:
- 6 times 4 is 24
- 6 times 20 is 120
- 24 plus 120 is 144
How this method is different:
- it reinforces place value understanding
- it is similar to the way most people multiply in their head
- it is easy to explain
- it has a mathematical future, as it correctly uses place value, expanded notation, and the distributive property:
- 6 x 24 = 6(20 + 4) = 120 + 24 = 144
- it gets students ready for algebraic processes: 6(y + 4) = 6y + 24
- it also requires students to know, and practice, how to multiply with multiples of 10 (as in 6 times 20 is 120)
What about bigger numbers?
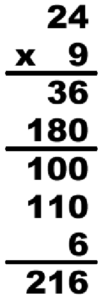 Don’t we eventually have to carry?
Don’t we eventually have to carry?
Let’s take a look at 9 x 24.
Here’s the sequence of steps:
- 9 times 4 is 36
- 9 times 20 is 180
- at this stage, if you can’t see that the sum is 216, you can use partial sums:
- add the hundreds to get 100
- add the tens to get 110
- add the ones to get 6
- altogether, that’s 216
Is there Multiplication v.3?
There are variations to the above method.
Whatever paper-and-pencil methods we decide children should learn, we should ensure that they are understandable and have a mathematical future.
- paper-and-pencil computational methods should build on children’s previous knowledge
- they should prepare children for more complex mathematics