Five As for coding + math
Related
Computational Thinking in Math Education Community of Practice @ Math Knowledge Network
Gadanidis, G. (in press). Five affordances of computational thinking to support elementary mathematics education. Journal of Computers in Mathematics and Science Teaching 36(2), 143-151.
Video transcript
 Today, there is a lot of pressure in our society to have young children to learn to code: from industry, from government, from academics in computer science, from non-profit and from for-profit organizations.
Today, there is a lot of pressure in our society to have young children to learn to code: from industry, from government, from academics in computer science, from non-profit and from for-profit organizations.
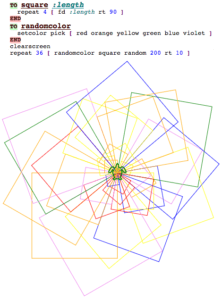 Coding is not new in education.
Coding is not new in education.
Forty, fifty years ago, Papert and his team developed Logo, which was an environment for young children to learn to code.
The difference between today and what we did in the past, is that we used to have a strong connection to mathematics. When Papert developed Logo, he said, learning math in Logo is like learning French by going to France.
 Coding and math are complementary subjects, and they are easy to integrate.
Coding and math are complementary subjects, and they are easy to integrate.
Coding on its own, is one more thing to teach in an already crowded curriculum.
Coding and math are a natural fit. In fact, coding offers 5 important affordances that help us teach mathematics better.
Agency
The first affordance is agency.
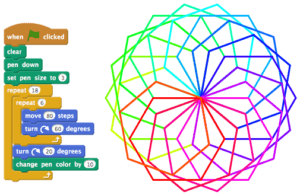 When children are working in a coding environment, the world is open to them. They can explore the activity that the teacher gave to them, but they can also ask what-if questions and try other things.
When children are working in a coding environment, the world is open to them. They can explore the activity that the teacher gave to them, but they can also ask what-if questions and try other things.
For example, when I was working in a grade 3 classroom, and this was the first time that this classroom did coding and mathematics, one of the young students came up to me and said, “I’m not going to do what you did on the screen, I’m going to do something of my own, and then I’m going to come afterwards and say to you, watch this!” That’s agency.
Access
The second affordance is access.
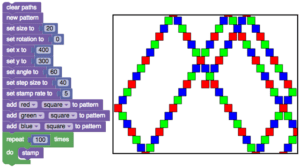 The beauty of the coding environments we have today, and the one that Papert developed with Logo, is that it has a low floor and a high ceiling.
The beauty of the coding environments we have today, and the one that Papert developed with Logo, is that it has a low floor and a high ceiling.
You can engage with coding, with minimal prerequisite knowledge. At the same time, you have the whole coding environment available to you, so you can do very complex programming as well.
So you can explore mathematics ideas that are quite simple, or quite complex. This is what we mean by differentiated instruction. Students can enter at their level, and work to their potential.
Abstraction
The third affordance is abstraction.
When you want, for example, to teach the computer to draw a square on the screen, you need to know what a square is, you need to know its essential characteristics.
You can put the block in of walk forward 100 steps, turn right, and put a loop around it, do this 4 times, and that would create a square. So what you’ve done there, you created the essential characteristics of a square, and you can even take that and create a new block called draw square.
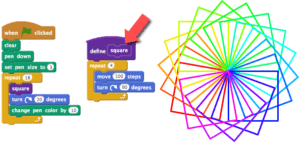 And then you can take this block and use it as an object of other things you write, so you can put it in another repeat loop, you can make it turn around, you can make it spin, you can make it do a variety of patterns. So what coding does is not only does it help you create abstractions, but those abstractions have a concrete feel, because they are objects on the screen that you can manipulate.
And then you can take this block and use it as an object of other things you write, so you can put it in another repeat loop, you can make it turn around, you can make it spin, you can make it do a variety of patterns. So what coding does is not only does it help you create abstractions, but those abstractions have a concrete feel, because they are objects on the screen that you can manipulate.
Making mathematical abstractions have a concrete feel, also makes them more accessible to young children.
Automation
The fourth affordance is automation.
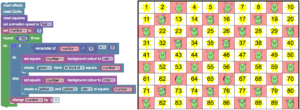 Normally what you would do if you were working with pencil and paper, you would draw one sketch out and then you want another variation of that, well you have to draw it again.
Normally what you would do if you were working with pencil and paper, you would draw one sketch out and then you want another variation of that, well you have to draw it again.
But in a coding environment, you have your code, and you can say well I would to do this a little bit different, and change one little parameter, and then all you have to do is press on start and then it does it for you.
You’ve automated that process, you can try it over and over, you can show it to others, you can ask what-if questions, change this, see what happens, all very quickly. So it allows for that dynamic modeling, and that exploration, that normally you wouldn’t be able to do.
Audience
The last affordance is that of audience.
 Audience is very important for learning for young students because they love to share ideas, they love to see the ideas of others, and you can do this very easily in a coding environment. It’s digital so you can share with parents at home, you can share with peers, and you can access the ideas of others and build on them.
Audience is very important for learning for young students because they love to share ideas, they love to see the ideas of others, and you can do this very easily in a coding environment. It’s digital so you can share with parents at home, you can share with peers, and you can access the ideas of others and build on them.
 Video ends with animated clip of Talk Math to your Computer.
Video ends with animated clip of Talk Math to your Computer.
10 affordances of computational modelling
Components of the above 5 affordances described above may be subcategorized to create a list of 10 affordances that come into play when computational tools are used to model mathematical concepts and relationships:

