LIKE CATERPILLARS TEACHING BUTTERFLIES TO FLY

Ideas for discussing & disrupting conceptions of mathematics education.

by George Gadanidis, PhD

THOSE WHO UNDERSTAND, TEACH?

Aristotle is credited with saying: Those who know, do. Those who understand, teach. Having a degree in mathematics, I started teaching knowing a lot of mathematics. However, in many cases my understanding lacked depth.

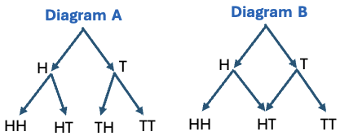
For example, if you had asked me which diagram, A or B, would be best for keeping track of outcomes when flipping 2 coins, I would have likely chosen B as the order of Heads and Tails does not matter. However, it was not until sometime later that I came to understand more of the mathematics behind this choice.

Isn’t it interesting that probability outcomes when flipping coins match number patterns in Pascal’s triangle and numeric coefficients in binomial power expansions (which leads to the Binomial Theorem)? These representations have in common binary choice: heads or tails, left or right, x or y.

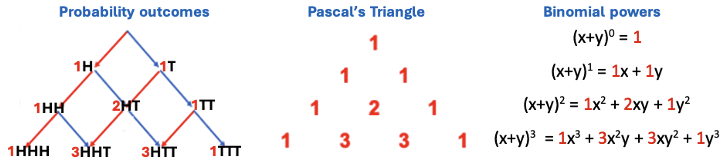
Knowing such connections between probability and algebra, educators can prioritize mathematical ideas that span across grades and better select representations that support conceptual understanding. For example, by using diagram B to keep track of outcomes, children as young as grades 1-2 can explain that HT is twice as likely as HH or TT, since there are two paths leading to HT.

When I have shared these ideas with educators, their response was like mine: a sense of surprise, along with the question: why didn’t we learn this in school?

Like caterpillars teaching butterflies to fly, we are sharing a shallow understanding of mathematics with children that deserve better.

DO WE UNDERESTIMATE CHILDREN?

There is a historical pattern dating back to ancient Sumer, where adults forget the wonder of their childhood and instead complain that the younger generation lacks math facts, writing ability, work ethic, manners, and so on. So, it is not surprising we are drawn to educational theories of what children cannot do, like Jean Piaget’s stages of cognitive development.

Piaget assumed young children do not have the capacity for abstract thinking until around age 11. Seymour Papert who worked with Piaget disagreed, noting that these stages are in the learning cultures we create and not in children’s minds. Kieran Egan added that young children would not be able to develop language if they could not abstract—such as, abstracting the essential characteristics of “dog” and telling it apart from other four-legged creatures.

Underestimating children helps perpetuate a lack of attention to mathematical depth.

In this age where we feed AI the best mathematics we have to offer, don’t children also deserve as much?

WHAT DID YOU DO IN MATH TODAY?

My deepest mathematical understanding developed while co-teaching in many classrooms, collaborating with educators to solve what Brian Boyd calls artistic puzzles in storytelling, to design and engage children with mathematical experiences that are worthy of human attention. For instance, for the topic of fractions in grade 3, we used fractional area patterns to bring infinity and limit to life, so children can learn to hold infinity in their hands!

See learnx.ca/mt/infinity-overview.

When children shared such learning at home, parents said: “I loved her excitement and complete understanding and explanation of it all” and “I was surprised how easily my son grasped it all”.

WHAT NEXT?

It’s best not to try to change everything at once. Rather, occasionally select, study and carefully implement experiences that engage children with mathematical depth, beauty and wonder, which, as John Dewey suggested, live fruitfully in future experiences by raising expectation and anticipation of what mathematics may offer.