From PEDAGOGY to MATHEMATICS, part 1: Why we can’t get there from here
(c) 2021 George Gadanidis, Western University
IT LOOKS GOOD BUT IS IT GOOD MATHEMATICS?
Imagine this scenario: You visit a mathematics classroom and you are excited to see student math work displayed on classroom walls, students working collaboratively on math tasks using a variety of materials, with the teacher monitoring progress and offering help and encouragement. Pedagogically, it looks like an ideal classroom. But when you join a couple of the groups and more closely observe their work you notice that the mathematics they are engaged with is shallow and incomplete.
What is the problem? How might it be addressed?
HOW AND WHAT WE TEACH
Schwab (1983) identified four commonplaces of education we typically address when we talk about curriculum, teaching and learning:
- teacher
- student
- milieu
- subject matter
Pedagogy – how we teach – can significantly impact the roles of teachers and students, and it can affect the teaching and learning milieu. However, pedagogy has much less effect on subject matter.
In this post I draw a distinction between pedagogy and mathematics:
Although pedagogy is extremely important, it cannot improve, or only superficially improves, shallow mathematics we bring to the classroom.
To illustrate this distinction between how and what we teach, I offer two examples of the geometry we typically bring to classrooms.
EXAMPLE 1: PARALLEL LINES
What mathematics do we teach?
What mathematics do we bring to the classroom when we teach about parallel lines?
For over 15 years, our mathematics teacher education program has included activities to disrupt prospective teachers’ conceptions of mathematics, as a form of math therapy (Gadanidis & Namukasa, 2005, 2007).
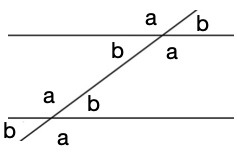
When we ask, “Tell me everything you know about parallel lines” prospective teachers typically share that “parallel lines are straight and they never meet.” A few also remember “something about transversals” and the angles that they create.
How might we teach these ideas?
A reasonable pedagogical approach may involve the following:
- Using a math scavenger hunt, students identify in the world around them lines that are parallel, as well as transversals.
- Students work in pairs to construct parallel lines and transversals, using paper and pencil or dynamic geometry tools, and identify, share and discuss patterns in angle measurements.
But the mathematics is still shallow
About 2,300 years ago, Euclid tried to prove his Parallel Lines Postulate but was unable to do so. Neither were mathematicians that followed. It turns out that the idea that “parallel lines never meet” is not a theorem to be proven. It is an assumption and different assumptions create different geometries.
This is roughly how Euclid looked at the problem:
We have a straight line and a point near the line. How many straight lines can we draw through the point that will not cross the first line?
Euclid wanted to prove that the answer is 1.
If the answer is “1” then we live on Flatland (a.k.a. Euclidean geometry).
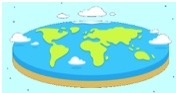
If the answer is “0” then we live on a sphere, where “parallel” lines “meet”. If we take a globe and create a “triangle” using the equator and 2 lines of longitude, the sum of interior angles can have many answers.

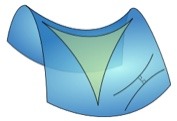
If the answer is “infinite” then we live on a hyperbolic surface.
More on parallel lines
Consider this riddle:
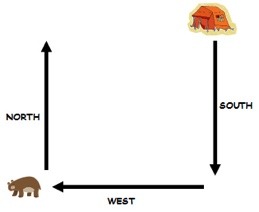
Molly steps out of her tent. Walks south 1 km. Walks west 1 km. Sees a bear. Runs north 1km, arriving back at her tent. How can this be? And what colour is the bear?
Not sure of the answer?
See an interview on the theme of parallel lines with Dr. Megumi Harada of McMaster University at imaginethis.ca/megumi-harada.

See also animated video #11, Parallel lines parallel universe, at imaginethis.ca/videos.

Read the story Parallel Lines.

The effect of what we teach
Here is a comment from preservice teachers in our teacher education program, reflecting on their school mathematics experience (Gadanidis & Namukasa, 2007):
I feel like I was misled, misguided, told the half-truth about parallel lines. It is the first time that I have realised and felt that math isn’t just BLACK & WHITE and can cause quite creative outcomes and discussions.
How is it possible that students learn parallel lines never meet when they live on a sphere?
Why would we think that the solution to shallow mathematics is better pedagogy when what is really missing is a good conceptual structure of the mathematics of parallel lines?
EXAMPLE 2: SYMMETRY
For millennia, symmetry was primarily used to describe the properties of shapes (Stewart, 2013), which is what most elementary school children learn about symmetry today (Healy, 2003). For example, the letter A has 1 line of symmetry and the letter H has 2 lines of symmetry.
Symmetry as a transformation
Over the last couple of centuries mathematicians have come to view symmetry not as an attribute but as a transformation that leaves an object apparently unchanged (Gadanidis, Clements & Yiu, 2018).
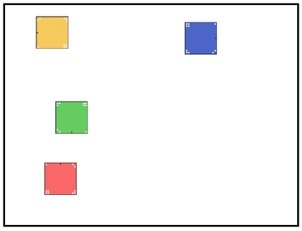
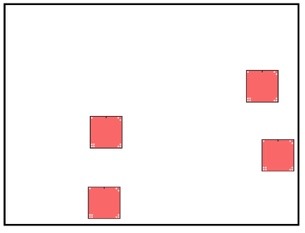
Looking at the image below, what transformation may have been applied to the square?

Once we see symmetry as a transformation, more interesting mathematics emerges.
When the ideas of symmetry we bring to the classroom are deeper, more mathematical, they create opportunities for surprise and insight – for wonder.
In GRADES 2-8 classroomS
I’ve had the pleasure of working with “symmetry as a transformation” in several grades 2-8 classrooms. When students combine the 4 rotation symmetries of the square, they notice that the result is always a rotation symmetry.
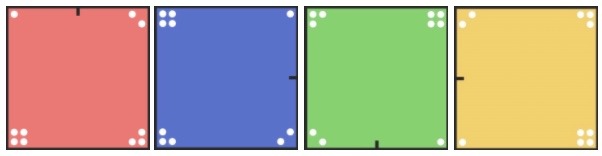
The rotation symmetries of the square are a tightly-knit group. They are happy spending time just with one another.
Students also notice that the 4 reflection symmetries of the square behave differently.

“When I put 2 reflections together I get a rotation.”
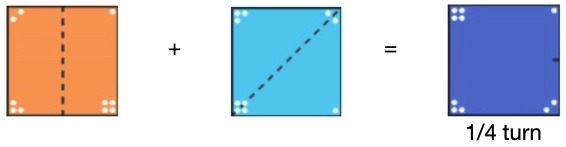
“Let’s try it with 2 different reflections.”

“It’s a rotation again!”
The reflection symmetries of the square also like to meet new symmetries when they transform one another.
Isn’t this wonderful?
different mathematical structures
When we rotate a square, all the rotation symmetries “live” on the same side of the square. The square never flips over.
When we reflect a square, the reflection “lives” on the other side. Reflecting a square twice (or any even number of times) brings it back to its rotation side.
Rotation symmetries and reflection symmetries are different mathematical structures.
You can also see this difference by labelling the vertices of the square 1-4 and recording how their number order changes. The image below shows the number order for each of the 4 rotation symmetries of the square: 0, 1/4, 1/2 and 3/4 turn.

See more about symmetries at https://learnx.ca/symmetry.
In a grade 6 classroom
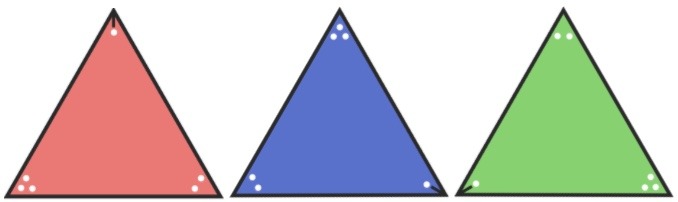
In a grade 6 classroom (Gadanidis, Clements & Yiu, 2018), after we worked with the symmetries of squares and triangles, we posed this problem:
Imagine we put the 4 rotation symmetries of the square in a rectangle and let them move and bump into one another, like bumper cars. Also imagine that when they bump they transform one another using their symmetries. For example, the 90o rotation symmetry would turn the 180o rotation symmetry another 90o and transform it to a 270o rotation symmetry. What might happen if we let them bump and transform one another in this way for a while?
As serendipity would have it, the first three student predictions were all correct but expressed differently:
- They will all become red
- They will all become 0o
- They will all become 360o
Why is this the case?
Try it yourself at learnx.ca/sym/bumper-squares.
Would the same thing happen if we used the 3 rotation symmetries of the equilateral triangle?
IN A STORY
Read the story Symmetry.

A BLINDSPOT
Teaching mathematics is not just about how we teach and how students learn. It is also about what mathematics we bring to the classroom.
We have become very good at pedagogy. We can walk into a classroom, or reflect on our own teaching, and recognize what works well pedagogically and what does not.
We also need to be able to recognize and be concerned about the quality of the mathematics we bring to the classroom.
__________________
Sequel to this post
In the sequel to this post I offer a model, with an example, for recognizing and designing better quality mathematics that we bring to classrooms.
__________________
References
Gadanidis, G, Clements, E. & Yiu, C. (2018). Group theory, computational thinking and young mathematicians. Mathematical Thinking and Learning 20(1), 32-53.
Gadanidis, G. & Namukasa, I. (2005). Math Therapy. The Fifteenth ICMI Study: The Professional Education and Development of Teachers of Mathematics, State University of Sao Paolo at Rio Claro, Brazil, 15-21 May 2005.
Gadanidis, G. & Namukasa, I. (2007). Mathematics-for-teachers (and students). Journal of Teaching and Learning, 5(1), 13-22.
Healy, L. (2003). From symmetry as a property to reflection as a geometrical transformation: Evolving meanings and computational tools. Paper presented at the Third Computer Algebra in Mathematics Education Symposium. Reims, France.
Schwab, J.J. (1983). The practical 4: Something for curriculum professors to do. Curriculum Inquiry, 13(3), 239-265.
Stewart, I. (2013). Symmetry. A very short introduction. Oxford, UK: Oxford University Press.